Scipy Linalg

SciPy是使用優化的ATLAS LAPACK和BLAS庫構建的。它具有非常快的線性代數能力。所有這些線性代數例程都需要一個可以轉換爲二維數組的對象。這些例程的輸出也是一個二維數組。

SciPy.linalg與NumPy.linalg

scipy.linalg包含numpy.linalg中的所有函數。另外，scipy.linalg還有一些不在numpy.linalg中的高級函數。在numpy.linalg上使用scipy.linalg的另一個優點是它總是用BLAS/LAPACK支持編譯，而對於NumPy，這是可選的。因此，根據NumPy的安裝方式，SciPy版本可能會更快。

線性方程組

scipy.linalg.solve特徵爲未知的x，y值求解線性方程a * x + b * y = Z。

作爲一個例子，假設需要解下面的聯立方程。
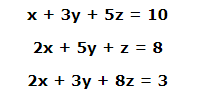
Scipy

要求解x，y，z值的上述方程式，可以使用矩陣求逆來求解向量，如下所示。
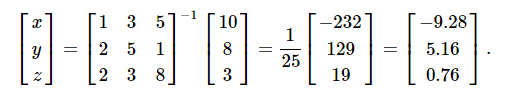
Scipy

但是，最好使用linalg.solve命令，該命令可以更快，更穩定。

求解函數採用兩個輸入'a'和'b'，其中'a'表示係數，'b'表示相應的右側值並返回解矩陣。

現在來看看下面的例子。

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np

#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])

#Passing the values to the solve function
x = linalg.solve(a, b)

#printing the result array
print (x)

執行上面示例代碼，得到以下結果 -

[ 2. -2.  9.]

查找一個行列式

方陣A的行列式通常表示爲| A |並且是線性代數中經常使用的量。在SciPy中，這是使用det()函數計算的。它將矩陣作爲輸入並返回一個標量值。

下面來看看一個例子。

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np

#Declaring the numpy array
A = np.array([[1,2],[3,4]])

#Passing the values to the det function
x = linalg.det(A)

#printing the result
print (x)

執行上面示例代碼，得到以下結果 -

-2.0

特徵值和特徵向量

特徵值 - 特徵向量問題是最常用的線性代數運算之一。我們可以通過考慮以下關係式來找到方陣(A)的特徵值(λ)和相應的特徵向量(v)

Av = λv

scipy.linalg.eig從普通或廣義特徵值問題計算特徵值。該函數返回特徵值和特徵向量。

讓我們來看看下面的例子。

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np

#Declaring the numpy array
A = np.array([[1,2],[3,4]])

#Passing the values to the eig function
l, v = linalg.eig(A)

#printing the result for eigen values
print (l)

#printing the result for eigen vectors
print (v)

執行上面示例代碼，得到以下結果 -

[-0.37228132+0.j  5.37228132+0.j]
[[-0.82456484 -0.41597356]
 [ 0.56576746 -0.90937671]]

奇異值分解

奇異值分解(SVD)可以被認爲是特徵值問題擴展到非矩陣的矩陣。

scipy.linalg.svd將矩陣'a'分解爲兩個酉矩陣'U'和'Vh'，以及一個奇異值(實數，非負)的一維數組's'，使得a == U * S * Vh，其中'S'是具有主對角線's'的適當形狀的零點矩陣。

讓我們來看看下面的例子。參考以下代碼 -

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np

#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)

#Passing the values to the eig function
U, s, Vh = linalg.svd(a)

# printing the result
print (U, Vh, s)

執行上面示例代碼，得到以下結果 -

[[-0.60142679+0.28212127j  0.35719830-0.03260559j  0.61548126-0.22632383j]
 [-0.00477296+0.44250532j  0.64058557+0.15734719j -0.40414313+0.45357092j]
 [ 0.46360086+0.38462177j -0.18611686+0.6337182j   0.44311251+0.06747886j]] [[ 0.98724353+0.j         -0.01113675+0.15882756j]
 [-0.15921753+0.j         -0.06905445+0.9848255j ]] [ 2.04228408  1.33798044]

Scipy教程

線性方程組

查找一個行列式

特徵值和特徵向量

奇異值分解