Java技術Web開發高級語言其他技術腳本語言數據庫大數據教程XML技術專業教育框架軟件工具教程通信技術微軟技術軟件測試手機開發前端技術人工智能實例代碼

使用 Java 在二元搜尋樹中尋找節點的父節點

瀏覽人數：384最近更新：

    一、簡介

    二元搜尋樹（BST）是一種幫助我們有效解決現實世界問題的資料結構。

    在這篇文章中，我們將研究如何解決在 BST 中尋找節點的父節點的問題。

    2.什麼是二元搜尋樹？

    BST 是一棵樹，其中每個節點最多指向兩個節點，通常稱為左子節點和右子節點。此外，每個節點的值都大於左子節點且小於右子節點。

    例如，讓我們想像三個節點：A=2、B=1 和 C=4。因此，一種可能的 BST 將 A 作為根，B 作為其左子節點，C 作為其右子節點。

    在接下來的部分中，我們將使用透過預設insert()方法實現的 BST 結構來練習查找節點的父節點的問題。

    3. 二元搜尋樹中節點的父節點

    在下面的部分中，我們將描述在 BST 中尋找節點的父節點的問題，並練習一些解決該問題的方法。

    3.1.問題描述

    正如我們在整篇文章中所看到的，BST 的給定節點具有指向其左子節點和右子節點的指標。

    例如，讓我們想像一個具有三個節點的簡單 BST：

    使用

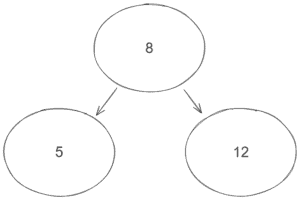
    節點8包含兩個子節點5和12 。因此，節點8是節點5和12的父節點。

    問題包括找到任何給定節點值的父節點。換句話說，我們必須找到其任何子節點等於目標值的節點。例如，在上圖中的 BST 中，如果我們在程式中輸入5 ，則我們期望輸出為8 。如果我們輸入12 ，我們也期望8 。

    此問題的邊緣情況是尋找最頂層根節點或 BST 中不存在的節點的父節點。在這兩種情況下，都沒有父節點。

    3.2.測試結構

    在深入研究各種解決方案之前，我們首先定義測試的基本結構：

    class BinaryTreeParentNodeFinderUnitTest {

 TreeNode subject;

 @BeforeEach
 void setUp() {
 subject = new TreeNode(8);
 subject.insert(5);
 subject.insert(12);
 subject.insert(3);
 subject.insert(7);
 subject.insert(1);
 subject.insert(4);
 subject.insert(11);
 subject.insert(14);
 subject.insert(13);
 subject.insert(16);
 }
 }

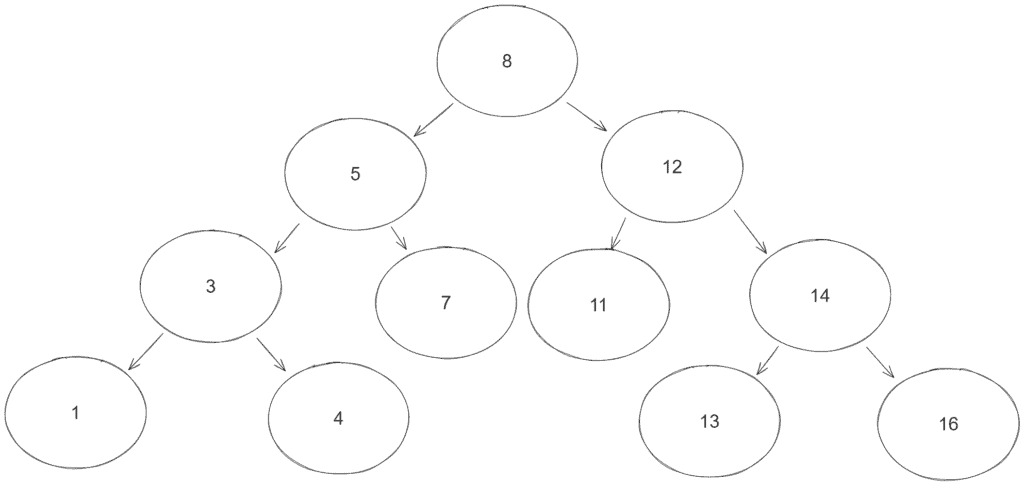
    BinaryTreeParentNodeFinderUnitTest定義了一個setUp()方法來建立以下 BST：

    使用

    4. 實作遞歸解決方案

    該問題的直接解決方案是使用遞歸遍歷樹並提前返回其任何子節點等於目標值的節點。

    我們首先在TreeNode類別中定義一個公共方法：

    TreeNode parent(int target) throws NoSuchElementException {
 return parent(this, new TreeNode(target));
 }

    現在，讓我們在TreeNode類別中定義parent()方法的遞歸版本：

    TreeNode parent(TreeNode current, TreeNode target) throws NoSuchElementException {
 if (target.equals(current) || current == null) {
 throw new NoSuchElementException(format("No parent node found for 'target.value=%s' " +
 "The target is not in the tree or the target is the topmost root node.",
 target.value));
 }

 if (target.equals(current.left) || target.equals(current.right)) {
 return current;
 }

 return parent(target.value < current.value ? current.left : current.right, target);
 }

    演算法首先檢查當前節點是否為最頂層的根節點或該節點是否不存在於樹中。在這兩種情況下，節點都沒有父節點，因此我們拋出NoSuchElementException.

    然後，演算法檢查目前節點子節點是否等於target 。如果是，則目前節點是目標節點的父節點。因此，我們返回current 。

    最後，我們根據target使用遞迴呼叫向左或向右遍歷 BST。

    讓我們測試一下我們的遞歸解決方案：

    @Test
 void givenBinaryTree_whenFindParentNode_thenReturnCorrectParentNode() {
 assertThrows(NoSuchElementException.class, () -> subject.parent(1231));
 assertThrows(NoSuchElementException.class, () -> subject.parent(8));
 assertEquals(8, subject.parent(5).value);
 assertEquals(5, subject.parent(3).value);
 assertEquals(5, subject.parent(7).value);
 assertEquals(3, subject.parent(4).value);
 // assertions for other nodes
 }

    在最壞的情況下，演算法最多執行n次遞歸操作，每次查找父節點的成本為O(1) ，其中n是 BST 中的節點數。因此，時間複雜度為O(n) 。在平衡良好的 BST 中，該時間降至O(log n) ，因為其高度始終最多為log n 。

    此外，此演算法使用堆空間進行遞歸呼叫。因此，在最壞的情況下，當我們找到葉節點時，遞歸呼叫就會停止。因此，該演算法最多堆疊h次遞歸調用，這使得其空間複雜度為O(h) ，其中h是 BST 的高度。

    5. 實施迭代解決方案

    幾乎任何遞歸解決方案都有迭代版本。特別是，我們也可以使用堆疊和while循環而不是遞歸來找到 BST 的父級。

    為此，我們將iterativeParent()方法加入到TreeNode類別：

    TreeNode iterativeParent(int target) {
 return iterativeParent(this, new TreeNode(target));
 }

    上面的方法只是下面輔助方法的介面：

    TreeNode iterativeParent(TreeNode current, TreeNode target) {
 Deque <TreeNode> parentCandidates = new LinkedList<>();

 String notFoundMessage = format("No parent node found for 'target.value=%s' " +
 "The target is not in the tree or the target is the topmost root node.",
 target.value);

 if (target.equals(current)) {
 throw new NoSuchElementException(notFoundMessage);
 }

 while (current != null || !parentCandidates.isEmpty()) {

 while (current != null) {
 parentCandidates.addFirst(current);
 current = current.left;
 }

 current = parentCandidates.pollFirst();

 if (target.equals(current.left) || target.equals(current.right)) {
 return current;
 }

 current = current.right;
 }

 throw new NoSuchElementException(notFoundMessage);
 }

    演算法首先初始化一個堆疊來儲存父候選。那麼主要取決於四個主要部分：

    1. 外部while循環檢查我們是否正在存取非葉節點或父候選堆疊是否不為空。在這兩種情況下，我們都應該繼續遍歷 BST，直到我們找到目標父代。
    2. 內部while循環再次檢查我們是否正在訪問非葉節點。此時，存取非葉節點意味著我們應該先向左遍歷，因為我們使用中序遍歷。因此，我們將父候選添加到堆疊中並繼續向左遍歷。
    3. 訪問左側節點後，我們從 Deque 輪詢一個節點，檢查該節點是否為目標的父節點，如果是則回傳。如果找不到父母，我們就會繼續往右移動。
    4. 最後，如果主循環完成而沒有傳回任何節點，我們可以假設該節點不存在或它是最頂層的根節點。

    現在，讓我們測試一下迭代方法：

    @Test
 void givenBinaryTree_whenFindParentNodeIteratively_thenReturnCorrectParentNode() {
 assertThrows(NoSuchElementException.class, () -> subject.iterativeParent(1231));
 assertThrows(NoSuchElementException.class, () -> subject.iterativeParent(8));
 assertEquals(8, subject.iterativeParent(5).value);
 assertEquals(5, subject.iterativeParent(3).value);
 assertEquals(5, subject.iterativeParent(7).value);
 assertEquals(3, subject.iterativeParent(4).value);

 // assertion for other nodes
 }

    在最壞的情況下，我們需要遍歷整棵o樹才能找到父節點，這使得迭代解的空間複雜度為O(n) 。同樣，如果 BST 是很好平衡的，我們可以在O(log n)中做同樣的事情。

    當我們到達葉節點時，我們開始從ParentCandidates堆疊中輪詢元素。因此，用於儲存父候選的附加堆疊最多包含h元素，其中h是 BST 的高度。因此，它也具有O(h)空間複雜度。

    6. 使用父指標建立 BST

    這個問題的另一個解決方案是修改現有的 BST 資料結構來儲存每個節點的父節點。

    為此，我們建立另一個名為ParentKeeperTreeNode的類，其中包含一個名為parent的新欄位：

    class ParentKeeperTreeNode {

 int value;
 ParentKeeperTreeNode parent;
 ParentKeeperTreeNode left;
 ParentKeeperTreeNode right;

 // value field arg constructor

 // equals and hashcode
 }

    現在，我們需要建立一個自訂insert()方法來儲存父節點：

    void insert(ParentKeeperTreeNode currentNode, final int value) {
 if (currentNode.left == null && value < currentNode.value) {
 currentNode.left = new ParentKeeperTreeNode(value);
 currentNode.left.parent = currentNode;
 return;
 }

 if (currentNode.right == null && value > currentNode.value) {
 currentNode.right = new ParentKeeperTreeNode(value);
 currentNode.right.parent = currentNode;
 return;
 }

 if (value > currentNode.value) {
 insert(currentNode.right, value);
 }

 if (value < currentNode.value) {
 insert(currentNode.left, value);
 }
 }

    當為目前節點建立新的左或右子節點時， insert()方法也會儲存父節點。在這種情況下，由於我們正在建立一個新的子節點，因此父節點始終是我們正在存取的目前節點。

    最後，我們可以測試儲存父指標的 BST 版本：

    @Test
 void givenParentKeeperBinaryTree_whenGetParent_thenReturnCorrectParent() {
 ParentKeeperTreeNode subject = new ParentKeeperTreeNode(8);
 subject.insert(5);
 subject.insert(12);
 subject.insert(3);
 subject.insert(7);
 subject.insert(1);
 subject.insert(4);
 subject.insert(11);
 subject.insert(14);
 subject.insert(13);
 subject.insert(16);

 assertNull(subject.parent);
 assertEquals(8, subject.left.parent.value);
 assertEquals(8, subject.right.parent.value);
 assertEquals(5, subject.left.left.parent.value);
 assertEquals(5, subject.left.right.parent.value);

 // tests for other nodes
 }

    在這種類型的 BST 中，我們在節點插入期間計算父節點。因此，為了驗證結果，我們可以簡單地檢查每個節點中的父引用。

    因此，我們可以在O(1)時間內透過引用立即取得它，而不是在O(h)中計算每個給定節點的parent() 。此外，每個節點的父節點只是對記憶體中另一個現有物件的引用。因此，空間複雜度也是O(1) 。

    當我們經常需要檢索節點的父節點時，該版本的 BST 非常有用，因為parent()操作已經經過了很好的最佳化。

    七、結論

    在那篇文章中，我們看到了尋找 BST 的任何給定節點的父節點的問題。

    我們透過程式碼範例練習了該問題的三種解決方案。一種方法是使用遞歸來遍歷 BST。另一個使用堆疊來儲存父候選並遍歷 BST。最後一個在每個節點中保留一個父引用，以在恆定時間內獲取它。

    與往常一樣，原始碼可以在 GitHub 上取得。

    本作品係原創或者翻譯，採用《署名-非商業性使用-禁止演繹4.0國際》許可協議

    最新文章

    Java 周刊，第 538 期尋找給定年份的復活節星期日的日期MongoRepository 中使用 Limit 和 Skip 的不同方式在 Java 中尋找 URL 的重定向 URL重寫 toString() 方法時列印預設值求最長對稱子串的長度給定 URL 從 S3 下載文件Java 中的迭代器與 forEach()探索 Java 中的複數算術運算Gson 的多態性