在N元樹中打印給定節點的同級

給定N元樹和元素X，任務是打印值為X的節點的同級對象。

如果兩個節點位於同一級別且具有相同的父節點，則將其視為同級。

例子：

輸入： X = 100， 輸出： 90和110
說明：值為90、100和110的節點具有相同的父節點，即值為40的節點。因此，節點90和110是給定節點X（= 100）的同級節點。

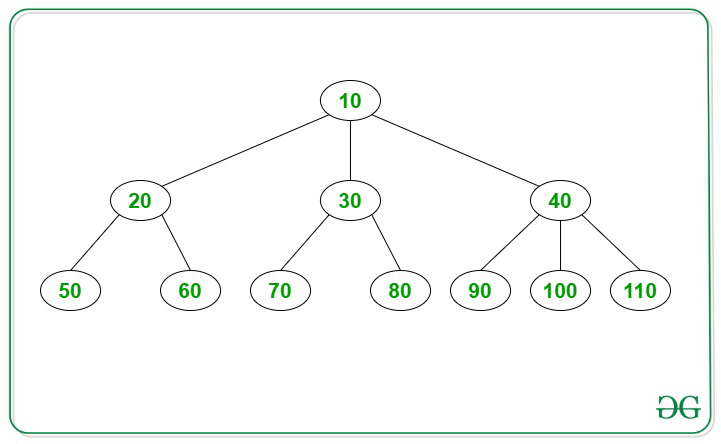
輸入： X = 30, 輸出： 20和40
說明： 值為20、30和40的節點具有相同的父節點，即值為10的節點。因此，節點20和40是給定節點X（= 30）的同級節點。

方法：按照以下步驟解決問題：

1. 在給定的N元樹上執行級別順序遍歷
2. 初始化隊列q以進行級別順序遍歷
3. 對於遇到的每個節點，將其所有子節點推入隊列。
4. 在推動當前節點的孩子到隊列中，請檢查：如果這些孩子是等於給定值X與否。如果發現為真，則將除X之外的所有其他節點打印為當前子級，作為所需答案。
5. 否則，繼續遍歷樹。

// C++ program for the above approach 
#include <bits/stdc++.h> 
using namespace std; 

// Structure of a node of N-ary tree 
struct Node { 
    int key; 
    vector<Node*> child; 
}; 

// Function to create a new node 
Node* newNode(int key) 
{ 
    Node* temp = new Node; 
    temp->key = key; 
    return temp; 
} 

// Function to find the siblings 
// of the node value 
void Siblings(Node* root, int value) 
{ 
    int flag = 0; 

    if (root == NULL) 
        return; 

    // Stores nodes level wise 
    queue<Node*> q; 

    // Push the root 
    q.push(root); 

    // Continue until all levels 
    // are traversed 
    while (!q.empty()) { 

        // Stores current node 
        Node* temp = q.front(); 
        q.pop(); 

        // Enqueue all children of the current node 
        for (int i = 0; i < temp->child.size(); i++) { 

            // If node value is found 
            if (temp->child[i]->key == value) { 

                flag = 1; 

                // Print all children of current node 
                // except value as the answer 
                for (int j = 0; j < temp->child.size(); 
                    j++) { 

                    if (value 
                        != temp->child[j]->key) 
                        cout << temp->child[j]->key 
                            << " "; 
                } 
                break; 
            } 

            // Push the child nodes 
            // of temp into the queue 
            q.push(temp->child[i]); 
        } 
    } 

    if (flag == 0) 
        cout << "No siblings!!"; 
} 

Node* constructTree() 
{ 
    Node* root = newNode(10); 
    (root->child).push_back(newNode(20)); 

    (root->child).push_back(newNode(30)); 

    (root->child).push_back(newNode(40)); 

    (root->child[0]->child).push_back(newNode(50)); 

    (root->child[0]->child).push_back(newNode(60)); 

    (root->child[1]->child).push_back(newNode(70)); 

    (root->child[1]->child).push_back(newNode(80)); 

    (root->child[2]->child).push_back(newNode(90)); 

    (root->child[2]->child).push_back(newNode(100)); 

    (root->child[2]->child).push_back(newNode(110)); 

    return root; 
} 

// Driver Code 
int main() 
{ 

    // Stores root of the 
    // constructed tree 
    Node* root = constructTree(); 

    int X = 30; 
    // Print siblings of Node X 
    Siblings(root, X); 

    return 0; 
}

輸出：

20 40

時間複雜度： O（N 2）
輔助空間： O（N）