計算 Pi 的 Java 程序

一、概述

Pi 是圓的周長與該圓的直徑之比。不管任何圓的大小，pi的值大約等於3.14159。適用於圓的計算。

在本教程中，我們將了解如何使用 Java 計算 pi。我們將採用蒙特卡洛算法來解決這個任務。

2. 蒙特卡洛算法

Pi 是一個無理數——它不能用簡單的分數或定小數表示。我們可以使用各種數學方法將 pi 計算到任何所需的精度水平。

首先，蒙特卡洛方法是用於估計 pi 值的方法之一。這種方法使用隨機抽樣來獲得數學問題的數值解。

例如，假設我們有一個空畫布。接下來，讓我們在畫布上畫一個正方形，在正方形裡面畫一個大圓圈。然後，讓我們在正方形內生成隨機點。有些點落在圓圈內，有些落在圓圈外。為了估計 pi，我們將計算點的總數和圓內的點總數。下 圖描述了正方形、隨機生成的點和內切圓：

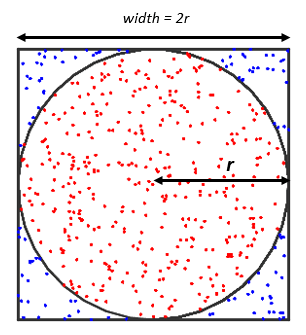
我們知道，圓的面積是 pi 乘以半徑的平方，而與圓內接的正方形的面積是四乘以半徑的平方。如果我們用圓的面積除以與圓內切的正方形的面積，我們將得到 pi 除以四。該比率也適用於正方形內的點數和封閉圓內的點數。

因此，讓我們看看使用蒙特卡洛方法估計 pi 的公式：

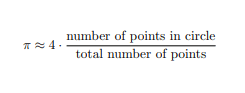
接下來，我們將使用 Java 實現該公式。

3. Pi Java程序

讓我們看一個使用蒙特卡洛算法計算 pi 的簡單 Java 程序：

@Test
 void givenPiCalculator_whenCalculatePiWithTenThousandPoints_thenEstimatedPiIsWithinTolerance() {
 int totalPoints = 10000;
 int insideCircle = 0;

 Random random = new Random();
 for (long i = 0; i < totalPoints; i++) {
 double x = random.nextDouble() * 2 - 1;
 double y = random.nextDouble() * 2 - 1;
 if (x * x + y * y <= 1) {
 insideCircle++;
 }
 }
 double pi = 4.0 * insideCircle / totalPoints;
 assertEquals(Math.PI, pi, 0.01);
 }

在上面的示例中，我們在以原點為中心的邊長為 2 的正方形內生成 10000 個隨機點。

接下來，我們檢查單個點以查看它是否落在圓圈內。距原點 1 以內的任何點都算作在圓內。

最後，我們通過計算圓內點數與點總數的比率並將結果乘以四來估算 pi 的值。

4。結論

在本文中，我們學習瞭如何使用蒙特卡洛算法估計 pi 的值。雖然還有其他一些數學方法可以估算 pi，但蒙特卡洛方法在 Java 中簡單易行。

與往常一樣，該示例的完整示例源代碼可在 GitHub 上獲得。