Java 中任意長度二進位整數的算術運算
1. 概述
在數位訊號處理中,通常會對訊號的二進位表示形式執行運算。在電腦圖形學中,位元操作對於顏色、像素操作和轉換至關重要。密碼學廣泛使用位元級操作來高效、安全地執行加密和雜湊函數。在所有這些情況下,處理任意長度的二進制數至關重要。
在本教程中,我們將了解在 Java 中對二進制數執行任意精確度算術運算的方法,探索BigInteger類別的使用以及BigInteger不可用或不需要的環境的替代方法。
我們也將研究二進製文字的限制。這對於闡明為什麼我們不能使用 Java 的基本類型以及負二進制數如何表示非常重要。
2. 二進位文字的位數
我們可以使用二進位文字將以二進位補碼表示法編寫的二進位整數指派給 32 位元Integer或 64 位元Long 。值得注意的是,Java API(例如Integer.toBinaryString()和Long.toBinaryString()也使用二進位補碼表示法。
補碼表示法意味著正數以2為基數書寫,而負數則透過添加2 32 (如果它們是Integer或2 64 (如果它們是Long )來書寫。這與以 32 位元或 64 位元寫入的無符號負數,反轉所有位元並加1完全相同。
讓我們嘗試一個簡單的測試:
@Test
void givenTwoBinaryLiterals_whenAdding_thenResultIsCorrect() {
int a = 0b110100101101010;
int b = 0b1000;
int expected = 0b110100101110010; // Result of a + b in binary
assertEquals(expected, a + b, "The addition of a and b should be correct");
}由於負數的補碼表示法,寫負數較不直觀。讓我們以-8為例:
@Test
void whenComparingBinaryToDecimal_thenValuesAreEqual() {
int c = 0b11111111111111111111111111111000; // (2^32 - 8) written in base 2
int expected = -8;
assertEquals(expected, c, "The binary value does not equal the decimal value of -8");
}二進位文字的主要問題是最大位數。這是 Eclipse 的螢幕截圖:

因此,如果我們需要執行任意精確度的算術運算,則二進位文字不是一個選擇。然而,當我們實現任意長度的二進制數之間的減法時,我們剛剛看到的負數的二進制補碼表示形式將再次派上用場。
3. 任意長度的二進位整數
任意長度的二進位整數可以由0和1組成的String物件表示,也可以由BigInteger物件表示。
總的來說, BigInteger是最簡單、最完整、最不容易出錯的解決方案。使用BigInteger時,我們不必使用二進位補碼表示法。相反,我們可以透過指定符號( +或– )後面跟著其絕對值來書寫數字。這是我們以10為基數的日常表示法表示數字的常用方式。如果數字是正數,我們可以省略+號:
@Test
void givenTwoBigIntegers_whenAdding_thenResultIsCorrect() {
BigInteger a = new BigInteger("1101001011010101010101010101010101010101010101010101010101010101010", 2);
BigInteger b = new BigInteger("-10000", 2);
BigInteger expected = new BigInteger("1101001011010101010101010101010101010101010101010101010101010011010", 2);
assertEquals(expected, BigIntegerExample.add(a, b), "The addition of a and b should be correct");
}但是,在某些特殊情況下BigInteger不可用。例如, Java ME CLDC 8用於機器對機器 (M2M) 和物聯網 (IoT) 設備,但它不包括BigInteger 。在這些情況下,從頭開始實現任意精確度的二進位算術,就像我們在BinaryStringOperations類別中所做的那樣,可以幫助我們解決特定場景,並且還具有教育價值。它使我們能夠加深對低階操作和二進制算術基礎知識的理解,而這些基礎知識通常被高級庫抽象化。
由於BinaryStringOperations類別大部分是不言自明的,因此我們將只討論程式碼中最相關的部分。
3.1.符號表示和測試
在我們的 JUnit 測試中,數字a長度為 67 位,超過了long基元類型允許的最大長度 64 位。 BinaryStringOperations中數字的符號的表示方式與BigInteger類似:
@Test
void givenTwoBinaryStrings_whenAdding_thenResultIsCorrect() {
String a = "1101001011010101010101010101010101010101010101010101010101010101010";
String b = "-10000";
String expected = "1101001011010101010101010101010101010101010101010101010101010011010"; // Expected result of a + b
assertEquals(expected, BinaryStringOperations.add(a, b), "The addition of a and b should be correct");
}至於我們測試的預期結果,我們用bc來計算,以確保我們沒有犯任何錯誤:
$ bc -l
[...]
ibase=2
obase=2
1101001011010101010101010101010101010101010101010101010101010101010 + -10000
1101001011010101010101010101010101010101010101010101010101010011010我們對其他操作的測試具有相同的結構。
3.2.四種操作的整體結構
BinaryStringOperations類別中的add() 、 subtract() 、 multiply()和divide()方法共用以下常見的結構屬性:
- 驗證 → 一些輔助方法確保輸入是有效的二進位字串
- 符號處理→我們使用
removePlusMinus(),使用isPositive()確定數字的正性,並確保結果中傳回正確的符號 - 基於符號的條件邏輯 → 這些方法包含條件語句,根據輸入字串是正數還是負數處理不同的場景
- 輔助方法 → **
unsignedAdd()、unsignedSubtract()、unsignedMultiply()和unsignedDivide()實作核心位元運算和計算邏輯
** - 邊緣情況處理 → 我們對邊緣情況實施了特殊處理,例如除以零
下面我們來看看如何將這些結構屬性應用到add()方法中:
static String add(String a, String b) {
String unsignedA = removePlusMinus(a);
String unsignedB = removePlusMinus(b);
if (isPositive(a)) {
if (isPositive(b)) {
// Example: a=1011, b=1111
return unsignedAdd(unsignedA, unsignedB);
} else {
// Example: a=1011, b=-1111
return subtract(unsignedA, unsignedB);
}
} else {
if (isPositive(b)) {
// Example: a=-1011, b=1111
return subtract(unsignedB, unsignedA);
} else {
// Example: a=-1011, b=-1111
return '-' + unsignedAdd(unsignedA, unsignedB);
}
}
}subtract() 、 multiply()和divide()方法遵循類似的結構,以確保有符號二進位字串運算的一致處理。
3.3. unsignedAdd()
unsignedAdd()方法執行兩個無符號二進位字串的加法。其演算法類似於手動二進制加法,從右到左逐位完成,根據需要處理進位位。
程式碼中的註解使各個步驟變得清晰:
static String unsignedAdd(String a, String b) {
validateUnsignedBinaryString(a);
validateUnsignedBinaryString(b);
// Remove leading zeros
a = a.replaceFirst("^0+(?!$)", "");
b = b.replaceFirst("^0+(?!$)", "");
int length = Math.max(a.length(), b.length());
// Pad the shorter string with leading zeros to make both strings of equal length
a = String.format("%" + length + "s", a).replace(' ', '0');
b = String.format("%" + length + "s", b).replace(' ', '0');
StringBuilder result = new StringBuilder(length * 2);
boolean carry = false;
// Iterate from the LSB (least significant bit) to the MSB (most significant bit)
for (int i = length - 1; i >= 0; i--) {
// Determine the bit values of the current position for both strings
boolean v1 = (a.charAt(i) == '1');
boolean v2 = (b.charAt(i) == '1');
// Calculate the result bit for the current position considering the carry
boolean r = carry && v1 && v2 || carry && !v1 && !v2 || !carry && v1 && !v2 || !carry && !v1 && v2;
// Update the carry for the next iteration
carry = carry && v1 || carry && v2 || v1 && v2;
// Insert the result bit at the beginning of the result string
result.insert(0, r ? '1' : '0');
}
// If there is a carry left, insert it at the beginning of the result string
if (carry) {
result.insert(0, '1');
}
return result.toString();
}程式碼中最困難的部分是位的計算:
boolean r = carry && v1 && v2 || carry && !v1 && !v2 || !carry && v1 && !v2 || !carry && !v1 && v2;
[...]
carry = carry && v1 || carry && v2 || v1 && v2;簡而言之,我們將位元計算的真值表寫在紙上,並將其複製到simplogic.dev中。然後它產生我們插入程式碼中的布林表達式。我們可以透過應用卡諾映射和德摩根定理手動獲得相同的表達式。
simplogic.dev也允許我們從程式碼中產生我們使用的真值表:
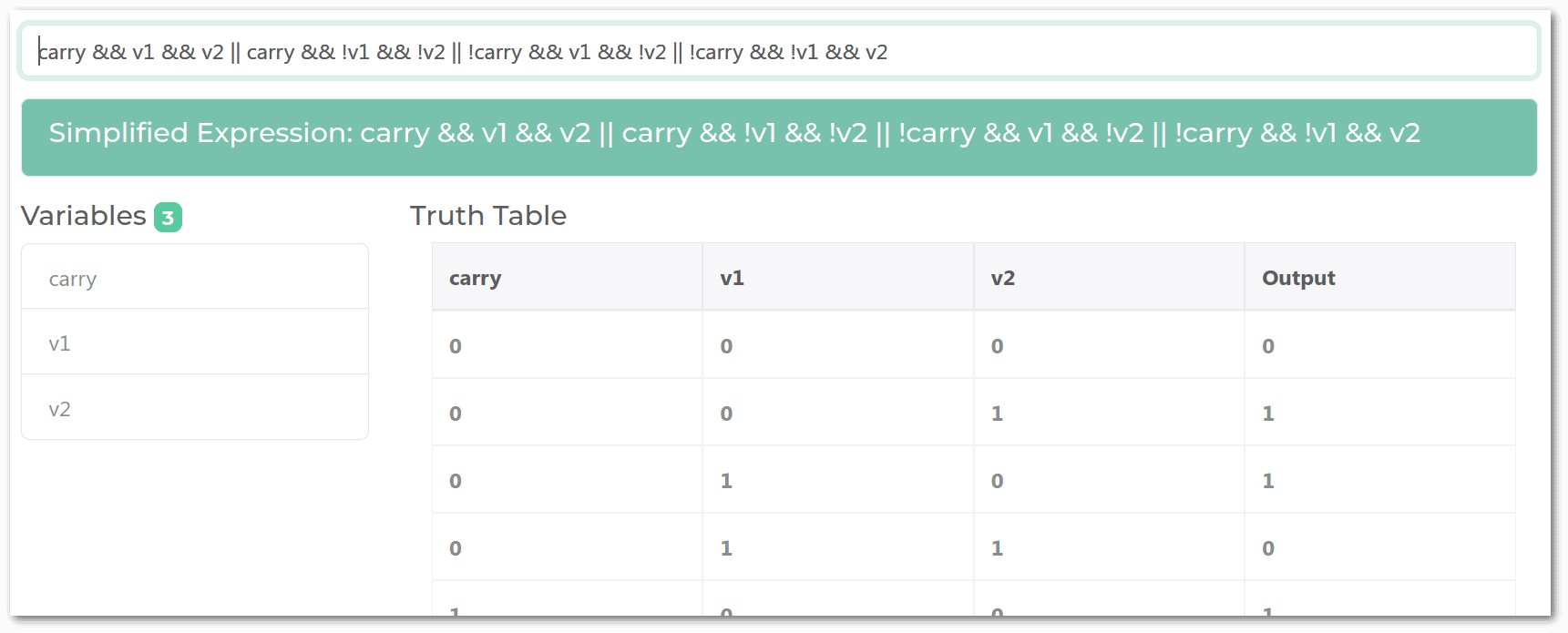
我們僅使用真值表進行求和。其他方法不需要它們。
3.4. unsignedSubtract()
我們使用二進制補碼進行減法,正如我們已經在二進位文字中看到的那樣。最簡單的方法是反轉b的位,加1 ,然後將該值加到a :
static String unsignedSubtract(String a, String b) {
[...]
// Two's complement step 1: invert all the bits
StringBuilder inverted = new StringBuilder();
for (int i = 0; i < b.length(); i++) {
char c = b.charAt(i);
if (c == '0') {
inverted.append('1');
} else {
inverted.append('0');
}
}
// Two's complement step 2: add 1 to the inverted bits
String b2complement = addOne(inverted.toString());
// Executes the sum between a and the two's complement of b
// Since a>=b, the result will always have an extra bit due to the carry out
// We remove this extra bit by using substring(1)
String result = unsignedAdd(a, b2complement).substring(1);
[...]
}透過二進制補碼減法,我們可以利用更簡單、更好理解的二進制加法過程,該過程只涉及進位,而不涉及借位。因此,使用二進制補碼可以降低減法運算的複雜性和出錯的可能性。
3.5. unsignedMultiply()
為了執行乘法,我們迭代b的位,並且對於設定為1每個位,我們將a的移位版本加入結果:
static String unsignedMultiply(String a, String b) {
[...]
// Iterate from the LSB (least significant bit) to the MSB (most significant bit) of "b"
for (int i = b.length() - 1; i >= 0; i--) {
zeros++;
if (b.charAt(i) == '1') {
// Calculate the partial product by appending the necessary number of zeros to "a"
// and this partial product is added to the result
result = unsignedAdd(result, appendZeros(a, zeros));
}
}
return result;
}這樣,我們將乘法視為一系列和,就像我們在手動計算中一樣。這降低了程式碼的複雜性。
3.6. unsignedDivide()
同樣,我們的演算法像手工一樣進行計算。我們迭代被除數的位,追蹤餘數,並透過在每一步將餘數與除數進行比較來建立結果:
static String unsignedDivide(String a, String b) {
[...]
// Iterate through each bit of the dividend "a" from MSB to LSB
for (int i = 0; i < a.length(); i++) {
if (result.length() == 0) {
// Initialize result and remainder if not yet done
if (compareBinaryStrings(a.substring(0, i + 1), b) >= 0) {
result.append('1');
remainder = unsignedSubtract(a.substring(0, i + 1), b);
}
} else {
// Concatenate the current bit of "a" to the remainder
remainder += a.charAt(i);
// Compare the current remainder with the divisor "b"
if (compareBinaryStrings(remainder, b) >= 0) {
// If remainder is greater than or equal to divisor, append '1' to result
result.append('1');
// Subtract divisor "b" from remainder
remainder = unsignedSubtract(remainder, b);
} else {
// If remainder is less than divisor, append '0' to result
result.append('0');
}
}
}
return result.toString();
}在此程式碼中,我們使用先前實現的減法來實現除法,而減法又使用加法。
3.7.程式碼優化?
我們的BinaryStringOperations類別為任意精度算術提供正確的演算法實作。如果我們沒有任何特殊的速度要求,那就沒問題。
然而, BigInteger類別明顯更加最佳化,具有先進且非常複雜的演算法,與我們可以從頭開始實現的基本方法相比,大大減少了執行時間。
4。
在本文中,我們探索了在 Java 中對二進制數執行任意精度算術運算的不同方法。我們討論了二進製文字的局限性,然後研究了BigInteger類別的使用。
我們也探索了使用BinaryStringOperations類別的任意精確度二進位算術的自訂實作。這種實現在BigInteger不可用的環境中或當我們想要深入研究位元操作的演算法挑戰時特別有用。
與往常一樣,完整的源代碼可以在 GitHub 上取得。